記述統計学(descriptive statistics)
記述統計学
『記述統計学』とは、データの集団に関する情報を整理し、要約し、理解しやすくするための手法や方法のことを指します。
記述統計学では、データの特徴や傾向(中心傾向やばらつき)などを収集、整理、分析するために、『代表値』や『散布度』が用いられます。
また、データのパターンや傾向を視覚的に理解するために『度数分布』などが用いられます。
- 代表値
データの中心的な値を示す指標になります。
代表値には主に『平均値』、『中央値』、『最頻値』の3つがあります。
- 散布度
データのばらつきや広がりを示す指標になります。
散布度には、『範囲』、『分散』、『標準偏差』のような指標があります。
- 度数分布
データを特定の範囲(区間)に分けて、それぞれの範囲に含まれるデータの数(頻度)を示す方法になります。
度数分布は、『度数分布表』や『ヒストグラム』を用いて視覚化されることが多くあります。
記述統計学の例として以下のようなものが挙げられます。
例えば、あるクラスの生徒20人のテストの点数データが以下のようになっているとします。
- 60点:3人
- 70点:5人
- 80点:6人
- 90点:4人
- 100点:2人
記述統計学では、このデータは以下のように整理されます。
- 代表値
- 平均値
- 点数の合計を人数で割った値です。例えば、(60×3 + 70×5 + 80×6 + 90×4 + 100×2) / 20 = 78点。
- 中央値
- 点数を小さい順に並べたときの中央の値です。この場合、20個のデータの真ん中の2つの平均、つまり80点と80点の平均で80点です。
- 最頻値
- 最も頻繁に出現する値です。この場合、80点が6人で最も多いので80点です。
- 平均値
- 散布度
- 範囲
- 最高点数と最低点数の差です。この場合、100点 - 60点 = 40点です。
- 分散
- データの平均値からのばらつき具合を示す指標です。この場合、76点になります。
- 標準偏差
- 標準偏差は分散の平方根であり、データのばらつきの大きさを示します。この場合、√76 ≒ 8.72点です。
- 範囲
- 度数分布
- 度数分布表
- 度数分布を示すために作成された表です。
- 度数分布表
| 点数の範囲 | 頻度 |
|---|---|
| 60 - 69 | 3 |
| 70 - 79 | 5 |
| 80 - 89 | 6 |
| 90 - 99 | 4 |
| 100 - 109 | 2 |
- ヒストグラム
- データの分布を視覚的に表現するために作成されたグラフです
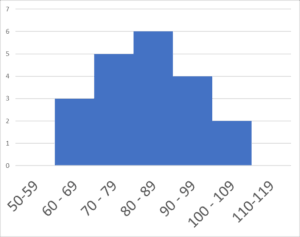
記述統計学は、このようにデータを理解しやすい形に整理し、分析するための基本的な手法になります。
参考・引用文献
\この記事を書いた人/
臨床心理士・公認心理師
上岡 晶
Ueoka Sho
精神科・心療内科での勤務を経て、2023年から「オンラインカウンセリングおはぎ」を開業しました。私のカウンセリングを受けてくださる方が少しでも望まれる生活を送れるように、一緒に歩んでいきたいと考えています。


